To err is human - and to blame it on a computer is even more so. Robert Orben
I sometimes write code as part of my research. My strategy is 'subtract and conquer': I verify my analytic calculations by subtracting it from an equivalent computation done by Wolfram Mathematica, hoping to get zero. So why don't I just use the Mathematica expression in the first place? Well, unfortunately Mathematica lacks intuition, and with some wits one can write a long Mathematica expression in a more satisfactory way for further analytic work and analysis.
Here you'll find a small part of the code I wrote for my research that I decided to share with the world.
Disclaimer: I have to admit that some of this code (especially the older stuff) is not very well commented. I hope you can still follow it despite this. Use it at your own risk...
Matlab
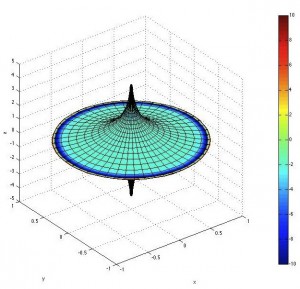
- GenerateSurface.m : GenerateSurface(SurfaceType, GridSize, Geodesic)
This program generates a 3D model of a surface (can be either a plane, sphere, pseudosphere, cylinder, cone, hyperboloid, saddle, torus or an exciting Möbius strip). The surface is colored according to the value of its scalar curvature. Moreover, the program allows you to control the grid size used for the surface (via the variable [GridSize]) and show a geodesic traveling on the surface by numerically solving the geodesic equation (in case the boolean [Geodesic] is set to true).
- SimulateOneSoliton.m : SimulateOneSoliton(Time, Space, dt, dz, PlotType, Periodic)
This programs solves Einstein's vacuum equation in the case considered for the Belinski-Zakharov transform. Since the metric is completely determined by the value of the two-by-two matrix g, its four components are the output of the program. The surface has [Time] temporal size and [Space] spatial size, with differential grid elements of length [dt] and [dz] respectively. The variable [PlotType] can be either '3D' in which the equation is solved numerically, 'Exact' in which the exact one soliton solution is generated or 'Error' that shows the deviation between the numerical and the exact solution. [Periodic] is a boolean that determines whether we use periodic boundary conditions.
Despite its name, one can modify the initial condition inside the function to obtain a numerical solution for any initial conditions.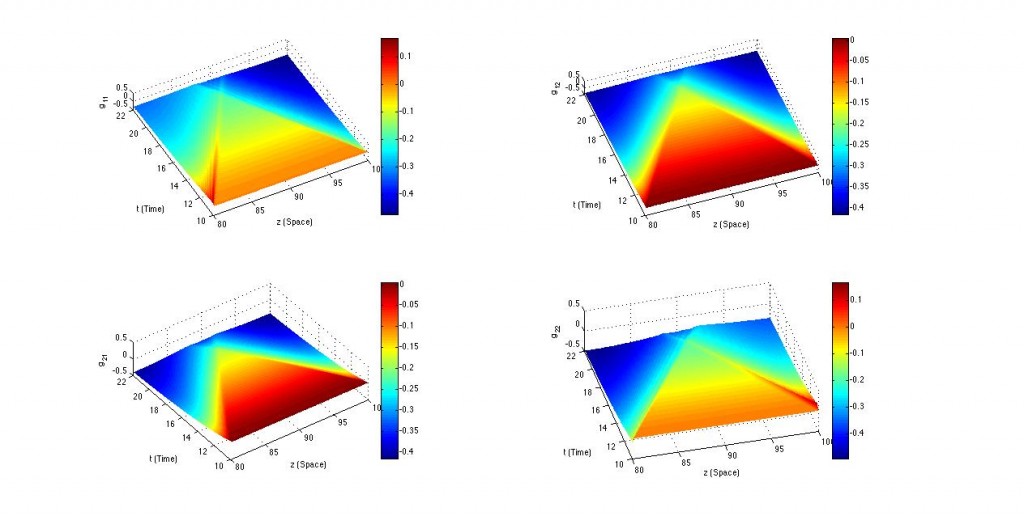
Recent Comments